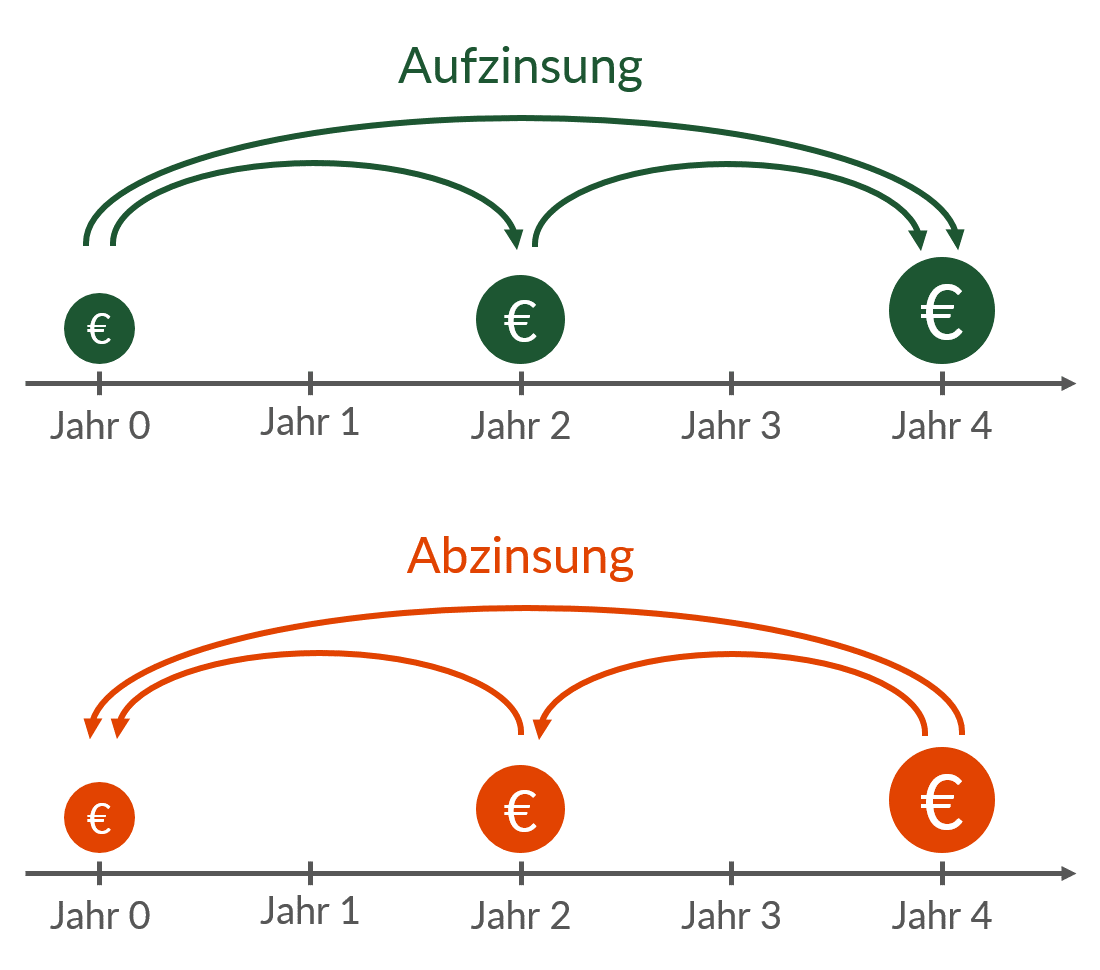
Aufzinsen und Abzinsen einfach erklärt (mit Rechenbeispiel)
Sobald du dich mit dynamischen Verfahren der Investitionsrechnung beschäftigst (z. B. Kapitalwert oder Annuitäten), wirst du zwangsläufig aufs Abzinsen und Aufzinsen stoßen. Sie sind die zentralen Instrumente, wenn du dich mit Zahlungen beschäftigst, die zu unterschiedlichen Zeitpunkten anfallen. Sie bilden die Basis für viele andere Rechenmethoden.
Und das Beste: Aufzinsen und Abzinsen ist im Grunde gar nicht so kompliziert, es wirkt im ersten Moment nur verwirrend. Mit ein bisschen Übung wirst du die Rechnung im Schlaf anwenden können.
Das erwartet dich in diesem Erklärtext
Wozu braucht man das Aufzinsen und Abzinsen?
Lass uns dazu ein kleines Beispiel anschauen: Stell dir vor, dein Chef bietet dir für deine gute Arbeit eine Bonuszahlung an. Entweder erhältst du heute 5000 Euro oder in drei Jahren 6000 Euro. Wie entscheidest du dich?
Bei deiner Überlegung sollen individuelle Argumente nicht zählen (etwa „Ich brauche dringend neue Möbel, also nehme ich jetzt 5000 Euro.“ oder „Ich bin sehr geduldig und nehme lieber die 6000 Euro.“).
Du willst rein ökonomisch wissen: Welche Variante ist mehr wert?
Die 6000 Euro sind zwar die höhere Zahl, dafür musst du noch lange darauf warten. Die 5000 Euro könntest du hingegen sofort nutzen und investieren, sodass du drei Jahre lang Zinsen und Zinseszinsen kassierst. Hast du auf diesem Weg in drei Jahren sogar mehr als 6000 Euro?
Für exakt diese Situationen kannst du die Aufzinsung bzw. Abzinsung nutzen. Sie helfen dir dabei, den Wert eines Geldbetrags auf einen anderen Zeitpunkt zu übertragen. Mit anderen Worten:
Was ist ein Geldbetrag ein, zwei, drei… Jahre früher wert? (Abzinsung)
Was ist ein Geldbetrag ein, zwei, drei… Jahre später wert? (Aufzinsung)
In unserem Beispiel könntest du also berechnen, was die 6000 Euro, die du in drei Jahren bekommst, heute wert sind. Diese Summe könntest du dann problemlos mit den 5000 Euro vergleichen. Dann nutzt du die Abzinsung.
Umgekehrt könntest du die 5000 Euro auf den Zeitpunkt „in drei Jahren“ umrechnen, um sie mit den 6000 Euro zu vergleichen. Dann wäre das Aufzinsung.
Wie berechnet man eine Aufzinsung?
Genug Theorie, lass uns rechnen. Wir wollen wissen, was die 5000 Euro in drei Jahren wert sind. Dazu wird immer davon ausgegangen, dass das Geld investiert werden kann und jedes Jahr Zinsen und Zinseszinsen anfallen. Der Betrag wird also schrittweise größer.
Wie hoch der Zinssatz ist, ergibt sich in der Praxis aus verschiedenen Faktoren, z.B. dem aktuellen Leitzins oder der Marktsituation. In den Prüfungsaufgaben der IHK (z.B. beim Wirtschaftsfachwirt) ist der Wert immer vorgegeben. Er wird als Kalkulationszinssatz bezeichnet.
Lass uns für das Beispiel einen Zinssatz von 6 Prozent annehmen. Mit dieser Information können wir aufzinsen. Dazu verwendet man folgende Grundformel:
\(\text{Aufgezinster Wert} = \text{Ursprungswert} \cdot \text{Aufzinsungsfaktor}\)Der Aufzinsungsfaktor berechnet sich wiederum mit dieser zweiten Formel:
\(\text{Aufzinsungsfaktor} = (1 + i)^n = q^n\)Was bedeuten die einzelnen Buchstaben? Klein i bezeichnet den Kalkulationszinssatz (in unserem Fall 6 Prozent) und q steht für „1 + Kalkulationszinssatz“. Es dient also nur dazu, die Formel etwas zu verkürzen. Das klein n wiederum steht für die Anzahl der Jahre, um die der ursprüngliche Geldbetrag aufgezinst werden soll.
Statt Jahren können auch andere Zeiteinheiten genommen werden (z.B. Monate oder Quartale), das wäre aber eher ungewöhnlich.
Konkretes Rechenbeispiel zur Aufzinsung
So kannst du Schritt für Schritt eine Betrag aufzinsen:
Schritt 1: Aufzinsungsfaktor ermitteln
Wir haben einen Zinssatz von 6 Prozent bzw. 0,06 vorgeben. Außerdem setzen wir n = 3, da die 5000 Euro um 3 Jahre aufgezinst werden sollen. Wir wollen schließlich den Zeitpunkt erreichen, in dem du alternativ 6000 Euro vom Chef bekommen würdest.
Diese beiden Zahlen setzen wir in die Formel für den Aufzinsungsfaktor ein:
\(\text{Aufzinsungsfaktor} = (1 + i)^n = (1 + 0,06)^3 = 1,191016\)
Kleiner Bonustipp
Schau mal in die IHK-Formelsammlung. Dort findest du eine Tabelle, in der viele Aufzinsungsfaktoren schon vorgegeben sind. Du musst nur den richtigen Zinssatz und die Anzahl der Jahre heraussuchen und den Aufzinsungsfaktor ablesen. So sparst du dir etwas Rechnerei.
Schritt 2: Aufgezinsten Wert berechnen
Nun kannst du problemlos die Formel für den aufgezinsten Wert anwenden:
\( \text{Aufgezinster Wert} = 5000 \text{ €} \cdot 1,191016 = 5955,08 \text{ €} \)Was sagt dir dieses Ergebnis? Bei einem Kalkulationszinssatz von 6 % sind 5000 Euro in drei Jahren schon 5955,08 Euro wert.
Ganz praktisch gesprochen: Du legst deine 5000 Euro heute zu 6 % an und bekommst immer am Ende des Jahres deine Zinsen ausgezahlt. Diese ausgezahlten Zinsen behältst du auf dem Konto, damit sie auch Zinsen abwerfen (Zinseszins) und so weiter. Am Ende des dritten Jahres beträgt dein Kontostand 5955,08 Euro. So entwickelt sich das Geld im Laufe der Jahre:
| Zeitpunkt | 0 | 1 | 2 | 3 |
|---|---|---|---|---|
| Kontostand | 5000 | 5300 | 5618 | 5955,08 |
Das ist zwar deutlich mehr als zu Beginn, aber immer noch etwas weniger als 6000 Euro, sodass die 6000 Euro die bessere Alternative sind.
Wie funktioniert die Abzinsung?
Dieses Ergebnis können wir nun überprüfen, indem wir die Rechnung andersherum durchführen. Wir zinsen nicht mehr die 5000 Euro auf, sondern jetzt werden die 6000 Euro aus dem Jahr 3 auf den heutigen Zeitpunkt (Jahr 0) abgezinst.
Das Grundprinzip ist identisch. Jetzt gehen wir aber davon aus, dass dir Zinsen entgehen, da du das Geld erst in drei Jahren bekommst. Daher sind 6000 Euro in drei Jahren heute weniger wert als 6000 Euro, die du sofort bekommen würdest.
Um die 6000 Euro auf den heutigen Tag umzurechnen, brauchen wir wieder den Kalkulationszinssatz in Höhe von 6 Prozent. Hinzu kommen sehr ähnliche Formeln:
\( \text{Abgezinster Wert} = \text{Ursprungswert} \cdot \text{Abzinsungsfaktor} \)sowie
\( \text{Abzinsungsfaktor} = \frac{1}{(1 + i)^n} = \frac{1}{q^n}\)Im Prinzip wird die Aufzinsung einfach umgedreht und schon ergibt sich die Abzinsung. Deshalb können wir direkt unsere Zahlen einsetzen und die Rechnung durchführen.
Rechenbeispiel zur Abzinsung
Schritt 1: Abzinsungsfaktor ermitteln
Unser Kalkulationszinssatz bleibt bei 6 % = 0,06. Auch die Jahreszahl ist identisch (n = 3). Diesmal „starten“ wir in Jahr 3 und wollen auf den heutigen Tag, also Jahr 0, abzinsen. Das ergibt:
\( \text{Abzinsungsfaktor} = \frac{1}{(1 + 0,06)^3} = 0,839619\)
Kleiner Bonustipp
Auch hier lohnt sich ein Blick in die Formelsammlung. Viele Abzinsungsfaktor lassen sich ablesen und ersparen dir die Rechnerei. Allerdings ist die Rechnung mit ein bisschen Übung relativ schnell zu erledigen.
Schritt 2: Abgezinsten Wert berechnen
Nun kommt die zweite Formel ins Spiel, mit der du den abgezinsten Wert ausrechnen kannst:
\( \text{Abgezinster Wert} = 6000 \cdot 0,839619 = 5037,71 \text{ €} \)Das Ergebnis: 6000 Euro, die du in drei Jahren bekommst, sind bei einem Kalkulationszinssatz von 6 Prozent heute nur 5037,71 Euro wert. Schrittweise gerechnet ergibt sich diese Übersicht:
| Zeitpunkt | 3 | 2 | 1 | 0 |
|---|---|---|---|---|
| Kontostand | 6000 | 5660,38 | 5339,98 | 5037,71 |
Mit anderen Worten: Wenn du heute exakt 5037,71 Euro bekommst und sie zu 6 Prozent anlegst, hast du in drei Jahren 6000 Euro. Nochmal anders ausgedrückt: Wenn du 5037,71 Euro auf drei Jahre aufzinst, ergeben sich genau 6000 Euro (mit minimaler Rundungsdifferenz). Rechne das gerne als kleine Probe!
Die Zahlen bringen genau die gleiche Empfehlung wie unsere Abzinsung. Nimm lieber die 6000 Euro in drei Jahren, die sind mehr wert als 5000 Euro, die du heute bekommst.
* Bei den markierten Verweisen zu Amazon handelt es sich um Affiliate-Links. Wenn du darüber etwas kaufst, erhalte ich eine Provision für meine Empfehlung. Für dich ändert sich nichts, denn Preis, Lieferung etc. bleiben gleich. Herzlichen Dank für deine Unterstützung!

Darf ich mich kurz bei dir vorstellen?
Hallo, ich bin Fabian Trummer. Mein Ziel ist es, dir den IHK Fachwirt so einfach wie möglich zu gestalten. Dazu helfe ich dir mit verständlichen Erklärtexten, Lerntipps und Übungsaufgaben. Hört sich das gut an?
Diese Texte könnten dich interessieren
Das war noch längst nicht alles...
Auf Modulearn werden regelmäßig neue Themenpakete, Übungsaufgaben und Lerntipps veröffentlicht. Melde Dich jetzt zum Newsletter an, um nichts Wichtiges zu verpassen.